🎓View(MVPV)变换
type
status
date
slug
summary
tags
category
icon
password
最近觉得光看Yan的课程对知识点的感知程度不够,有些对于老师来说理所当然的基础知识,对我来说不是那么直观。因此,我打算配合虎书一起食用。
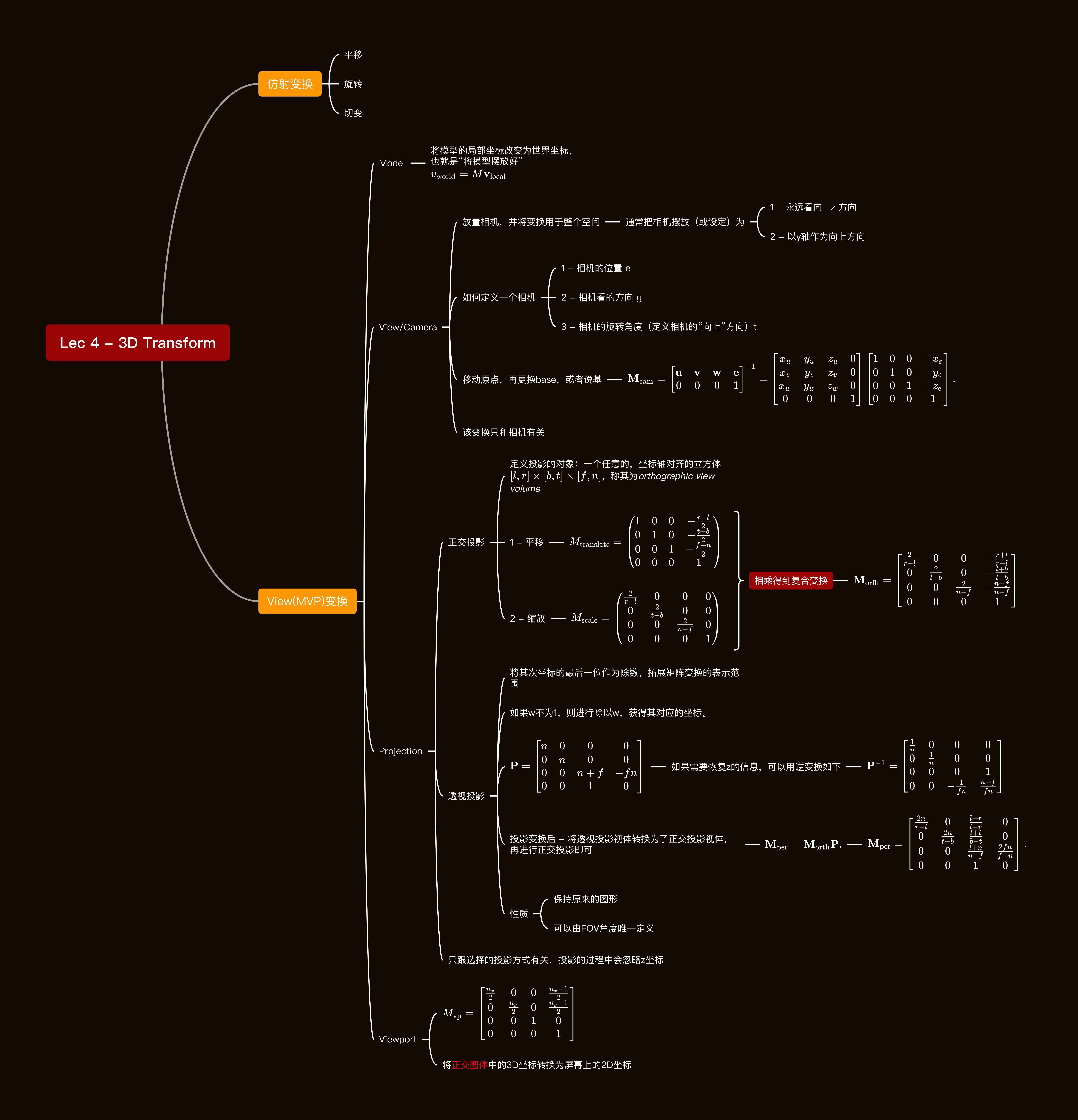
前言
所谓View变换,主要是对图像的顶点和线框(wireframe)进行变换,将其从3D的世界坐标转换为2D的屏幕坐标。

而这其中涉及到一些关键变换包括:
- Model Transformation,模型的局部坐标转换为世界坐标(其实就是摆放模型)。
- Camera(View) Transformation,将相机摆放在标准位置。
- Projection Transformation,将图像投影到[-1,1](x, y)的标准矩形当中。
- orthographic projection
- perspective projection
- Viewport Transformation(视口变换),将2D平面中的信息转换到屏幕上。
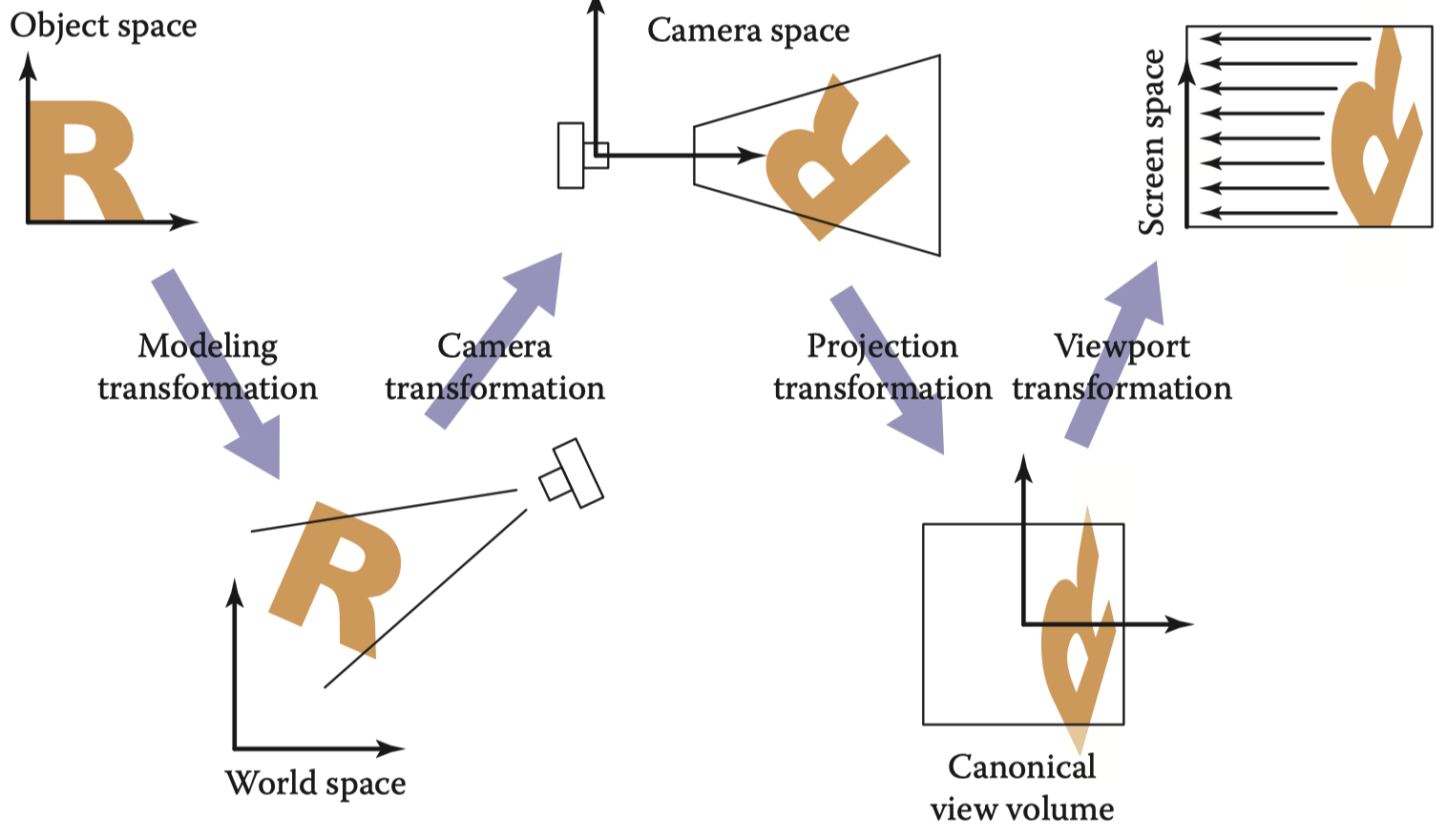
Camera Transformation
基本原理
相机变换(直译)的目标是将相机放在标准位置之上。
在虎书当中,相机由三个要素定义
- 位置
- 向上方向(top)
- 注视方向(gaze direction)
而标准位置的定义为:
- 相机的位置 与原点 重合
- 与 y 轴重合
- 看向 -z 方向
这样定义的好处有:
- 方便投影,保留xy即可。
- 方便进行后续的深度测试,因为z代表了深度。
根据相对运动的原理,我们只需要将世界中的其他顶点进行相同的变换,即可保证相机与物体之间的相对位置关系不变。
变换矩阵
很自然的,用语言描述想要的变换:
- 将相机放置在原点
- 旋转相机到标准位置
因此,将复合变换拆解成简单变换即可。
假设以目前相机所在位置,建设的坐标系为
平移矩阵可以轻松的写出:
而旋转矩阵是一个正交矩阵,根据矩阵变换的原理,我们可以写出
Projection Transformation
投影变换的过程会稍显复杂,但是不困难。
orthographic projection
我们将要投影的空间范围定义为轴对齐的立方体。
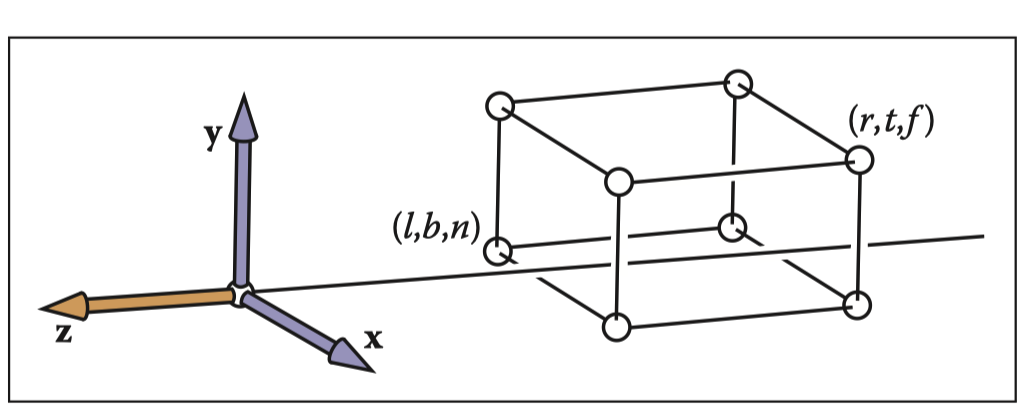
正交投影分为两个过程
- 移动到原点
- 缩放为标准立方体 [-1,1](x,y,z)
和相机变化的逻辑类似,我们可以轻易的写出正交投影的变换矩阵:
且
注意先后顺序,仿射变换先进行线性变换,再进行平移。
相乘得到复合变换
在🐯书当中,相机看向-z方向。因此,n > f。
perspective projection
基本原理
透视投影就比较复杂了,它与正交投影有一个明显的区别:
在距离观测点(eye/camera)越远的地方,物体越小,也就是近大远小。
而近大远小的直观体现,就是投影的大小随着z轴变动,即(x,y)与|z|成正比。
可以用相似三角形解释其原理:
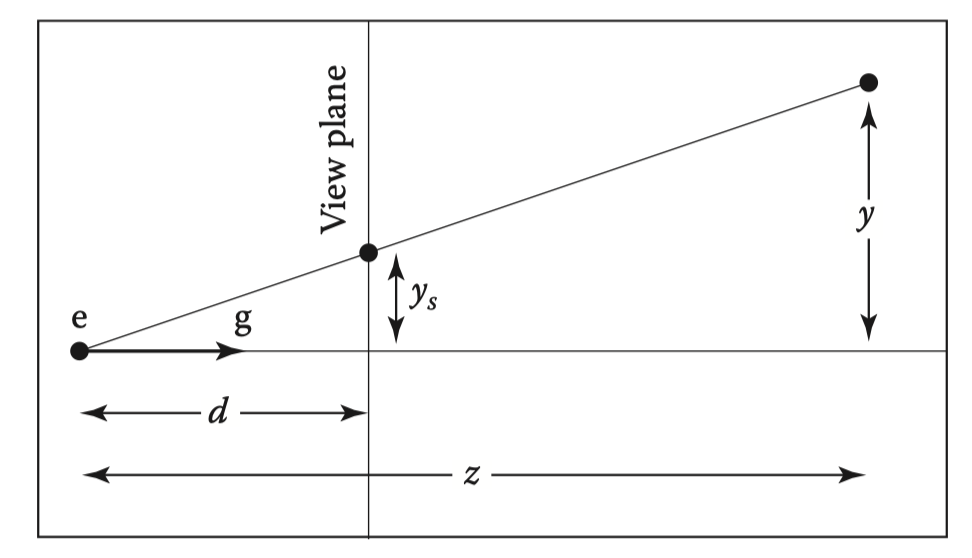
具体表现为:
如果我们能写出来一个变换矩阵,同时对(x,y)进行上述的变换,就可以轻松的解决透视投影的问题。
可惜,目前我们定义点/向量的方式无法支持除法操作。
拓展坐标表达
回顾三维空间中的点表达方式:
三维向量
使用的形式表达点。
这时,我们的变换矩阵仅能对该点进行线性变换,即:
齐次坐标
这时,使用的方式来表示点。
齐次坐标的引入,让我们可以进行仿射变换(先进行线性变换,后进行平移):
对齐次坐标进行拓展
我们定义一个点坐标,其表达的世界空间中的点为:
则我们引入了更多的变换:
同理,对于也会有类似的变换。
这样的变换有一个限制,坐标变换的除数是一样的!
变换矩阵
根据上述知识,我们可以凭借直觉写出一个可行变换矩阵:
如果将该矩阵进行乘法缩放,不会影响变换的效果,因为该矩阵同时对除数和被除数进行变换。
接下来,我们可以尝试写出二维形式的透视投影矩阵:
变换后,得到 ,即 ,实现了透视投影!
对于三维情况,我们假设n投影平面,f为远平面(类似正交投影的概念)。
写出矩阵:
前两行分别完成了对x,y的变换,第三行是对z的变换。
可能会有人疑惑,为什么对z的变换如此突兀,不自然,反直觉?
究其原因,是因为投影本身只需要保持(x,y)即可。
所以对z只有可用性的要求:
- n,f平面上的点的z坐标不变。
- z 需要保留其距离的语义,即支持通过对变换的的比对,判断出在世界空间中两点的深度。
因此,在虎书当中,给出的是这样一行z的变换,不同实现当中可能也有不同的表达,但是都应该满足上述两点需求。
变换举例:
经过这一变换,我们将一个截断的棱锥变为了一个轴对齐的立方体:
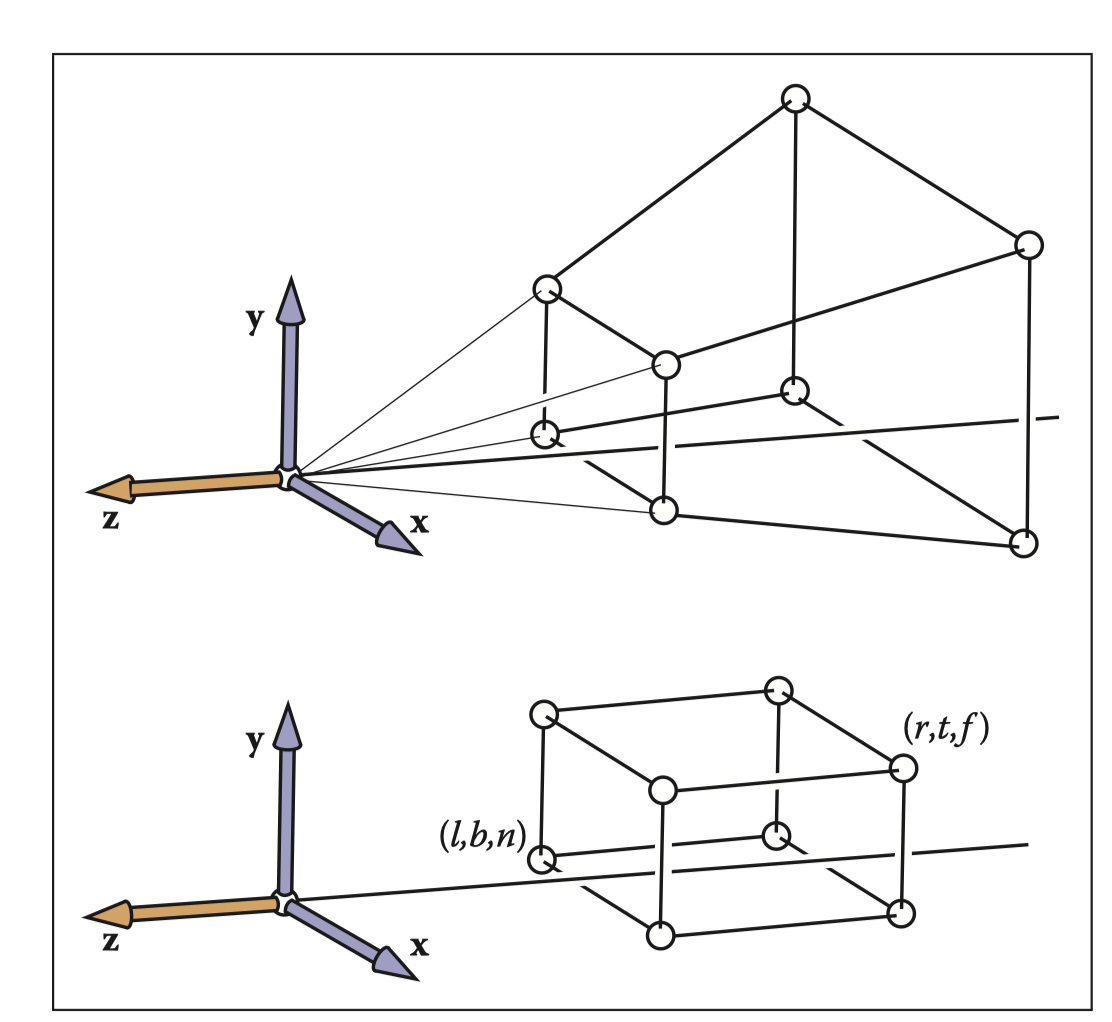
在完成透视变换后,直接衔接正交投影矩阵即可:
得到的变换矩阵如下:
看向-z方向,所以 n < f
有些时候,我们想获得投影点的原始世界坐标,直接进行逆变换即可:
逆变换矩阵
当然,根据之前提到过的性质,我们可以将其变的美观一些,放大
FOV(field-of-view)
如何定义一个透视投影区域?
f平面的宽高比应该和n平面的宽高比相同,因此,我们只需要额外获得透视角度的信息即可。
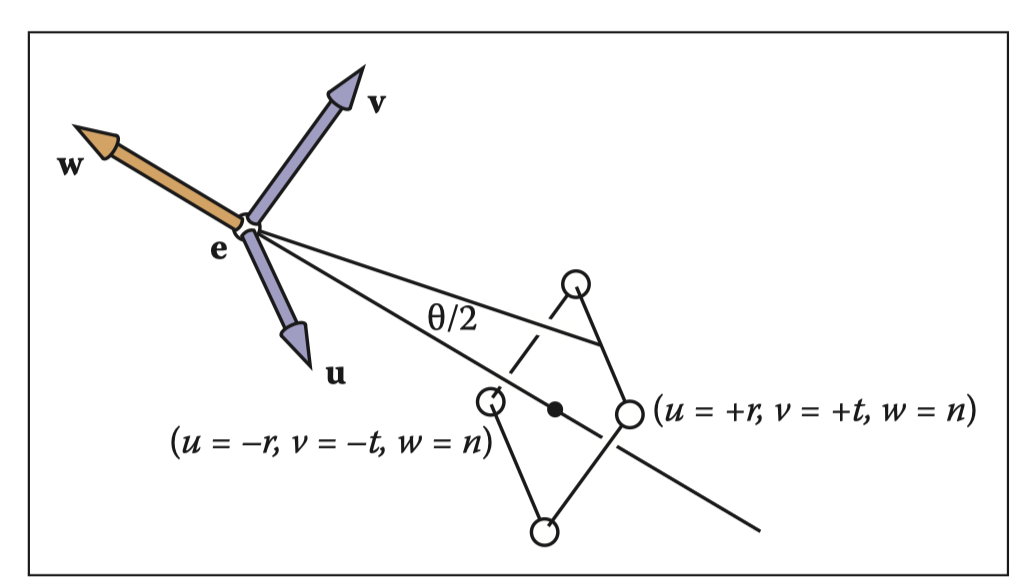
有了角度 ,我们就可以定义出完整的变换区域,根据:
Viewport Transformation
经过上述变换后,我们拥有了一个[-1,1](x,y,z)的标准视体,我们只需要将其投影到屏幕之上即可。
已知像素个数 ,分别表示x方向和y方向的像素个数。
一般起点为左下角,如果起点在右上方,旋转变换即可。
记得对像素点的定义,像素中心点位于整数坐标之上,是长度为1的正方形。因此,变换后的范围在之间,变换如下:
将长宽缩放,在进行移动,这是一个仿射变换,所以可以直接写出:
总结
至此,我们可以得到对没个顶点并行处理的变换矩阵:
基本的变换流程为:
🔗参考资料
- 《fundamentals of computer graphics 4th》
- 《games101》课程
上一篇
渲染管线(Pipeline)
下一篇
GAMES101 作业2
- Twikoo